[FFC 리뷰] Fast Fourier Convolution (NIPS 20)

My Summary & Opinion

앞의 다른 게시물에서도 말했다싶이, 나는 classic한 방법들을 network에 녹여낸 연구들을 좋아한다.

어떤 의도를 가지고 이러한 구조를 만들었는지가 명확하고, 그 성능도 명확히 보이기 때문이다.

그래서 이 논문을 엄청 재밌게 읽었다.

 

이 논문에서는 network에서 non-local한 연산을 진행하기 위해 FFT를 이용했다.

FFT를 해서 spectral domain으로 보내버리면 이미 그 자체로도 global하기 때문이다.

이처럼 FFC는 non-local할 뿐 아니라 one unit으로 구성되어있어, 기존의 모델들 안의 conv를 아무것도 수정하지 않고 FFC로 바꿀 수 있고, 성능 또한 더 좋아진다.

---

Introduction

Fast Fourier Convolution(FFC)를 설계할 때, 우리는 두가지를 고려했다.

첫번째는 CNN에서 중요한 부분은 receptive field라는 것이고, 두번째는 CNN은 chain-like topology라는 것이다.

그래서 우리는 non-local receptive field를 가지며 multi-scale information을 사용할 수 있는 방법을 찾았다.

이때 중요하게 생각한 것은 spectral transform theory다.

Fourier 이론에 의하면, spectral domain에서 한 값만 건드려도 전체 데이터에 영향을 준다.

그렇기 때문에 Fourier transform을 이용한 non-local을 만들었다.

또한, FFC는 아무것도 수정하지 않고 기존의 convolution을 대체할 수 있다는 장점이 있다.

---

Related Work

Non-local neural networks

Effective receptive field 이론에 의하면 convolution은 중심으로 쏠리는 경향이 있고, 그렇기 때문에 큰 conv kernel은 필요하지 않다.

하지만 작은 conv kernel은 over-fitting할 위험이 있다.

최근에는 한 층에서 서로 다른 neuron을 연결하는 것이 context-sensitive task에 중요하다는 것이 밝혀졌다.

 

Cross-scale fusion

CNN에 대해서 각각 다른 부분에서 다른 feature들이 추출된다는 것은 널리 알려져있다.

이 feature들을 concatenate해서 사용하는 것은 object ditection과 같은 분야에서 성능 향상에 도움이 된다.

 

Spectral neural networks

Spectral domain은 이전에는 convolution을 빠르게 하기위해서만 사용됐다면, 이제는 네트워크를 깊게 쌓는데도 도움이 된다.

우리는 spatial & spectral information을 이용해 mixed receptive field를 만들 것이다.

---

Fast Fourier Convolution (FFC)

Architectural Design

FFC는 두개의 inter-connected path로 이루어져있다.

Spatial(or local) path는 input feature channel에 대해서 기존의 convolution을 사용한다.

Spectral(or global) path는 spectral domain에서 작동한다.

각 path는 다른 receptive field에서 정보를 얻는다.

 

$X \in R^{H \times W \times C}$를 input feature map이라고 하자.

먼저 $X$를 feature channel을 따라 나눠서 $X={X^l, X^g}$로 만든다.

Local part인 $X^l \in R^{H \times W \times (1-\alpha_{in})C}$는 local neighborhood를 학습하기를 기대하고, global part인 $X^g \in R^{H \times W \times \alpha_{in}C}$는 long-range context를 학습하기를 기대한다.

네트워크를 간단하게 만들기 위해 output은 input과 같은 크기가 되도록 했다.

$Y={Y^l, Y^g}$는 다음과 같이 계산된다.

$Y^l=Y^{l \rightarrow l}+Y^{g \rightarrow l} = f_l(X^l)+f_{g \rightarrow l}(X^g)$

$Y^g=Y^{g \rightarrow g} +Y^{l \rightarrow g}=f_g(X^g)+f_{l \rightarrow g}(X^l)$

 

Implementation Details

1. Spectral transformer

위 그림에서의 global path의 목적은 convolution의 receptive field를 input feature map 전체로 확장시키는 것이다.

ResNet의 bottleneck block에 영감을 받아 computational cost를 줄이기 위해 $1 \times 1$ conv를 사용해서 채널을 반으로 나웠다.

다른 $1 \times 1$ conv는 feature channel dimenstion을 복원하기 위해 사용됐다.

이 두 conv 사이에는 global receptive field를 위한 Fourier Unit(FU)과 semi-global information을 위한 Local Fourier Unit(LFU)가 있다.

 

2. Fourier Unit (FU)

FU의 목적은 original spatial feature를 spectral domain으로 바꾸고, spectral data에 global update를 가한 후, 다시 spatial dobain으로 바꾸는 것이다.

아래 코드에 자세히 설명되어 있다.

 

3. Local Fourier Unit(LFU)

FU는 이미지 전체를 다룬다면, LFU는 semi-local information을 다룬다.

FU와의 가장 큰 차이점은 split-and-concatenate 과정이 추가됐다는 점이다.

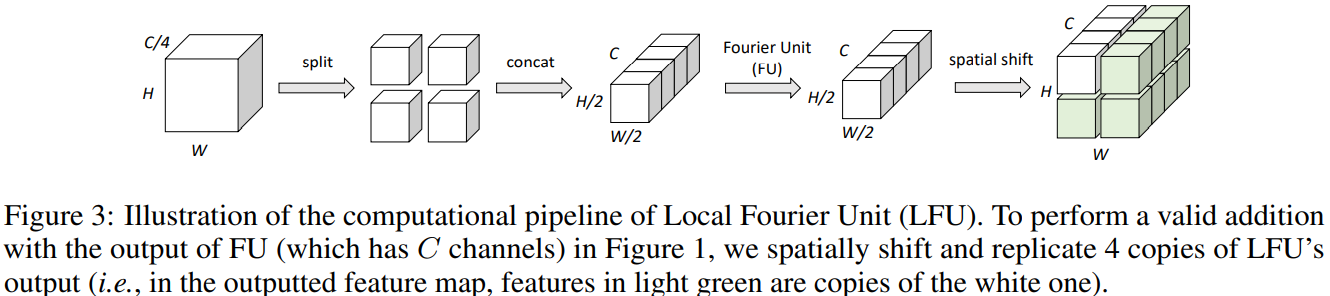
4. Compatibility with vanilla convolutions

$f_l, f_{g \rightarrow l}, f_{l \rightarrow g}$는 기존 conv로 되어있기 때문에 conv와 특성이 같다.

Spectral transformer $f_g$는 두가지 major consideration이 있다.

첫번째는 spectral domain이 이미 global receptive field기 때문에 큰 kernel size가 필요하지 않다는 것이다.

그래서 kernel size는 항상 1로 고정했다.

두번째는, 기존 conv의 downsampling를 흉내내기 위해 channel-reducing 단계 전에 average pooling을 진행한다.

 

Complexity analysis

FFT와 inverse FFT는 parameter-free이기 때문에 고려하지 않았다.

---

Experiments

단순히 기존 모델의 conv만 FFC로 바꿨을 뿐인데 성능이 좋아졌다.

---

Reference

Chi, Lu, Borui Jiang, and Yadong Mu. "Fast fourier convolution." Advances in Neural Information Processing Systems 33 (2020): 4479-4488.