[FSRCNN 리뷰] Accelerating the Super-Resolution Convolutional Neural Network (ECCV 16)

My Summary & Opinion

SRCNN을 만든 저자가 그 성능을 높이기 위해 만든 것이 FSRCNN(Fast-SRCNN)이다.

이름이 '빠른 SRCNN'인 것에서부터 알 수 있다시피 SRCNN의 속도를 높이는 데 중점을 뒀다.

 

ESPCN처럼 LR 이미지를 그대로 네트워크의 입력으로 넣고, 마지막에 upsampling 한다.

하지만 ESPCN이 Sub-Pixel Convolution layer를 사용한 것과 달리, deconvolution layer를 사용했다.

Convolution을 반대로 진행한다는 아이디어는 괜찮아 보이지만, Sub-Pixel Convolution의 콘셉트가 더 효율적으로 다가온다.

 

그 외에 shrinking & expanding layer도 시간을 줄이는데 효과적이겠지만, GPU가 발전한 요즘은 많이 쓰이지 않을 방법 같다.

---

Introduction

SR문제를 풀기 위해 deep-learning 방식이 주로 사용되고 있고, 그중 SRCNN은 간단한 구조와 좋은 성능으로 주목받았다.

SRCNN은 이전의 다른 learning-based 방법들과 비교했을 때 이미 충분히 빠르지만, 큰 이미지에서의 속도는 만족스럽지 않다.

 

네트워크 구조를 살펴보다가 속도를 제한하는 두 가지 원인을 발견했다.

첫째, LR 이미지는 bicubic upsampling 되어 네트워크에 입력으로 넣어진다.

이미지 크기를 $n$배 키웠다면 $n^2$만큼의 계산량이 늘어난다.

따라서 만약 input 이미지를 upsampling 하지 않고 그대로 사용한다면, $n^2$배만큼 빨라질 것이다.

 

둘째, SRCNN에서 input patch들은  high-dimensional LR feature space & HR feature space에 투영된다.

파라미터수가 많을수록 속도는 줄어들지만 그와 동시에 성능은 좋아진다.

문제는 '기존의 성능을 유지하며 어떻게 네트워크의 크기를 줄이느냐'이다.

 

위에서 언급한 두 가지 문제를 다음과 같이 해결함으로써 FSRCNN을 설계했다.

첫 번째 문제를 해결하기 위해 bicubic interpolation을 deconvolution layer로 바꿨다.

두 번째 문제를 해결하기 위해 mapping layer의 시작과 끝에 shrinking & expanding layer를 추가했다.

---

Related Work

1. Deep Learning for SR

SR 문제를 풀기 위해 처음 SRCNN이 제안된 후, 점점 더 깊은 구조들이 나오고 있다.

하지만 다른 모델들 모두 pre-processing 과정에서 bicubic interpolation을 진행해야 한다.

 

2. CNNs Acceleration

Object detection이나 image classification 등의 영역에서 CNN의 속도를 높이기 위한 많은 연구들이 진행됐다.

하지만 그 연구들은 high-level vision문제를 위해 고안된 것이다.

SR 문제를 위한 deep model들은 fully-connected layer가 없기 때문에 convolution filter의 역할이 중요하다.

---

Fast Super-Resolution by CNN

SRCNN을 간략히 설명한 후 어떻게 바꿨는지 설명한다.

 

1. SRCNN

자세한 설명은 이전 포스트에 써두겠다.

네트워크의 computation complexity는 다음과 같다.

$O{(f^2_1n_1 + n_1f^2_2n_2 + n_2f^2_3)S_{HR}}$

${f_i}^3_{i=1}$: the filter size, ${n_i}^3_{i=1}$: the filter number, $S_{HR}$: the size of the HR image

 

2. FSRCNN

FSRCNN은 5가지 부분으로 나눌 수 있다: feature extraction, shrinking, mapping, expanding, deconvolution.

앞의 4개는 convolution layer고, 마지막 하나는 deconvolution layer이다.

앞으로 convolution layer는 $Conv(f_i, n_i, c_i)$, deconvolution layer는 $DeConv(f_i, n_i, c_i)$라 표현한다.

$f_i$: the filter size, $n_i$: the number of filters, $c_i$: the number of channels

 

1) Feature Extraction

SRCNN의 첫 번째 layer의 filter 크기는 $9$다.

LR를 $Y_s$라 하고 interpolated $Y_s$를 $Y$라 하자.

$Y$에 있는 대부분의 pixel들은 $Y_s$에서 interpolated 된 것이므로, $Y_s$에서의 $5 \times 5$ patch는 $Y$에서의 $9 \times 9$ patch만큼을 커버할 수 있다.

그러므로 첫 번째 layer를 $Conv(5, d, 1)$로 정했다.

 

2) Shrinking

SRCNN의 mapping 단계에서 high-dimensional LR feature들은 바로 HR feature space에 mapping 된다.

이때 dimension $d$는 보통 매우 크기 때문에 계산량이 많아진다.

그러므로 $d$를 줄이기 위해 feature extraction단계 다음에 shrinking layer를 추가했다.

두 번째 layer는 $Conv(1, s, d)$이다. 이때, $s << d$이다.

이 과정을 통해 파라미터 수를 많이 감소시킨다.

 

3) Non-linear Mapping

Non-linear mapping은 SR 성능에 많은 영향을 끼치는 중요한 단계이다.

여기서 가장 영향을 많이 주는 것은 width(the number of filters in a layer)와 depth(the number of layers)이다.

SRCNN에서 $1 \times 1$ layer를 사용했을 때보다 $5 \times 5$ layer를 사용했을 때 성능이 더 좋았다.

이 실험을 바탕 삼아 더 효과적인 mapping layer를 고안했다.

네트워크의 크기와 성능 간에 trade-off가 있으므로 $f_3 = 3$으로 정했다.

그리고 SRCNN에서의 좋은 성능을 유지하기 위해 $3 \times 3$ layer를 여러 개 사용했다.

이렇게 Non-linear mapping layer는 $m \times Conv(3, s, s)$이다.

 

4) Expanding

Expanding layer는 shrinking layer와 정반대의 역할을 한다

Shrinking 과정은 계산을 위해 LR feature dimension을 줄이지만, 이렇게 low-dimensional feature들로 HR 이미지를 만들면 성능이 좋지 않다.

그래서 expanding layer를 추가했다.

Shrinking layer와 일관성을 유지하기 위해 $1 \times 1$ filter를 사용했다.

Shrinking layer가 $Conv(1, s, d)$인 것과 반대로, expanding layer는 $Conv(1, d, s)$이다.

 

5) Deconvolution

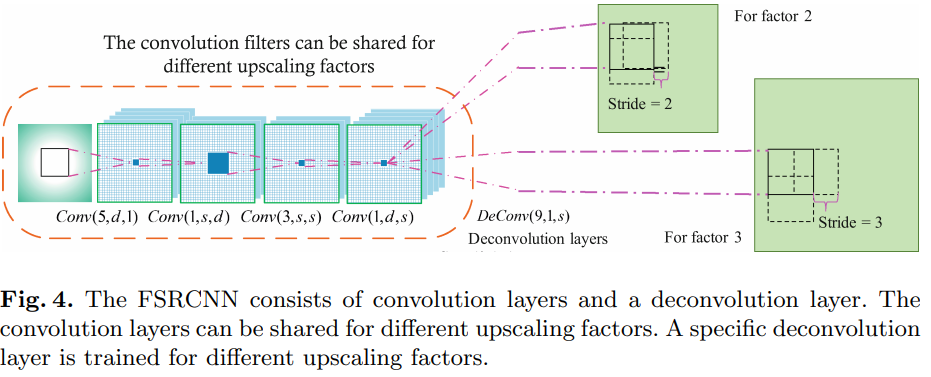
마지막 부분인 deconvolution은 deconvolution layer로 앞선 features를 upsample 하고 모아준다.

Deconvolution은 convolution 연산과 반대되는 연산이라고 볼 수 있다.

Stride $k$로 convolution을 진행하면 output은 input의 $1 \over k$ 크기가 된다.

만약 input과 output을 바꾸면, 위 그림처럼 output은 input의 $k$배가 될 것이다.

이처럼 네트워크를 반대로 생각해보면, reversed network는 HR 이미지를 받아 LR이 나오게 한다.

이처럼 deconvolution layer는 HR 이미지에서 feature를 추출하므로 $9 \times 9$ filter를 사용했다.

Deconvolution layer는 $DeConv(9, 1, d)$로 나타낸다.

이는 interpolation kernel들과는 달리 deconvolution layer는 upsampling kernel을 학습한다.

 

6) PReLU

ReLU를 사용할 때 zero gradient들로부터 만들어지는 'dead feature'를 없애기 위해 사용했다.

 

7) Overall Structure

$Conv(5, d, 1) - PReLU - Conv(1, s, d) - PReLU - m \times Conv(3, s, s) - PReLU -$

$Conv(1, d, s) - PReLU - Deconv(9, 1, d)$

FSRCNN의 computational complexity는 다음과 같다.

$O{(25d + sd + 9ms^2 + ds + 81d)S_{LR}} = O{(9ms^2 + 2sd + 106d)S_{LR}}$

 

8) Cost Function

MSE 사용했다.

 

3. Differences Against SRCNN: From SRCNN to FSRCNN

 

4. SR for Different Upscaling Factors

Deconvolution layer를 사용해서 속도를 높였다.

---

Experiments

속도도 빠르고 성능도 좋다.

---

Conclusion

SRCNN을 다시 설계함으로써 속도를 40배 빠르게 했다.

Real-time으로 사용될 수 있을 것이다.

---

Reference

Dong, Chao, Chen Change Loy, and Xiaoou Tang. "Accelerating the super-resolution convolutional neural network." European conference on computer vision. Springer, Cham, 2016.