[DnCNN 리뷰] Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising (IEEE TIP 17)

My Summary & Opinion

Gaussian denoising을 기반으로 해서 만든 모델은 처음이라 새로웠다.

다른 모델들처럼 단순히 층만 더 쌓았지만, 이를 수식적으로 풀어내 gaussian denoising으로 이해한 점이 흥미로웠다.

또한, 단순히 SISR뿐 아니라 JPEG artifact 제거도 잘 된다는 점이 흥미로웠는데, 이 둘의 artifact는 특성이 좀 다르기 때문이다.

---

Introduction

Image denoising은 오래됐지만 아직도 활발하게 연구되는 주제다.

대부분의 denoising 방법들은 두가지의 큰 단점이 있는데, 첫째는 복잡한 optimization 문제라는 것이고, 둘째는 non-convex하다는 것이다.

이런 문제를 극복하기 위해 다양한 방법들이 연구되었지만, 본 논문에서는 아래와 같은 이유로 CNN을 사용하고자 한다.

첫째, CNN을 깊게 쌓으면 이미지 특성을 충분히 고려할 수 있을 만큼 capacity와 flexibility가 늘어난다.

둘째, CNN을 학습시킬 때 사용하는 regularization과 learning method가 많이 발전됐다.

이런 방법들은 CNN이 더 빨리 학습되게 하고 더 좋은 성능을 보이게 한다.

 

본 논문에서 제안하는 DnCNN은 residual image인 $\mathbf{\hat{v}}$를 예측한다.

BN을 사용했을 때 DnCNN의 성능과 안정성이 높아졌다.

Contribution은 크게 세가지다.

1) Gaussian denoising을 위한 end-to-end CNN을 제안한다.

    기존의 CNN과 달리 residual image를 예측한다.

2) Residual learning과 BN을 사용하면 더 좋다.

3) Gaussian denoising 외의 JPEG deblokcing 등의 다른 노이즈에 대해서도 성능이 뛰어나다.

---

Related Work

Deep Neural Networks for Image Denoising

Multi-layer perceptron (MLP), trainable nonlinear reaction diffusion (TNRD), BM3D 등이 있다.

 

Residual Learning

Residual Learning은 원래 네트워크의 깊이가 깊어짐에 따라 생기는 성능 저하 문제를 해결하기 위해 제안됐다.

이로인해 깊은 CNN도 쉽게 학습된다.

Residual network들이 여러 residual unit들로 이루어진 것과 달리 DnCNN은 residual unit을 단 하나만 사용한다.

 

Batch Normalization

Mini-batch SGD는 CNN의 학습에 많이 사용됐지만, 이것의 simplicity와 effectiveness에도 불구하고 internalk covariate shift 때문에 학습 성능이 떨어졌다.

BN이 이를 해결한다.

---

The Proposed Denoising CNN Model

Network Depth

다른 연구(K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” in Proc. Int. Conf. Learn. Represent., 2015, pp. 1–14.)을 참고해서 Conv filter의 크기는 $3 \times 3$으로 고정했지만, pooling layer는 모두 지웠다.

그래서 깊이 $d$인 모델의 receptive field는 $(2d+1) \times (2d+1)$이 되어야한다.

 

DnCNN의 깊이를 정하기 위해 noise level을 $\sigma = 25$로 고정하고 여러가지 denoising 방법에서의 효과적인 patch 크기를 조사했다.

아래 표에는 noise level $\sigma = 25$일 때 제일 효과적인 patch 크기를 나타낸다.

아래 표를 보면 EPLL에서 효과적인 patch 크기는 $36 \times 36$으로 가장 작았다.

흥미롭게도, DnCNN은 EPLL과 비슷한 크기인 $35 \times 35$로 했을 때 그 성능이 제일 좋았다.

그래서 gaussian denoising을 위한 모델은 $35 \times 35$와 깊이는 17로 하고, 다른 일반적인 image denoising task를 위한 모델은 더 큰 patch를 사용하고 깊이는 20으로 했다.

 

 

Network Architecture

DnCNN의 input은 노이즈가 있는 $\mathbf{y = x + v}$다.

DnCNN에서 residual mapping을 학습시키기 위해 residual learning formulation $\mathcal{R}(\mathbf{y}) \approx \mathbf{v}$를 사용했다.

MSE로 표현하면 다음과 같다.

$l(\Theta) = {1 \over {2N}} \displaystyle \sum ^N_{i=1} ||\mathcal{R}(\mathbf{y_i}; \Theta) - (\mathbf{y_i} - \mathbf{x_i}) ||^2_F$

1. Deep architecture

깊이 $D$인 DnCNN은 아래 그림(fig. 1)처럼 세 종류의 layer가 있다.

$i$) Conv + ReLU: $64$ filters of size $3 \times 3 \times c$, (흑백일 때 $c=1$, 색이 있을 때 $c=3$)

$ii$) Conv + BN + ReLU: $3 \times 3 \times 64$

$iii$) Conv: $3 \times 3 \times 64$

 

2. Reducing Boundary Artifacts

대부분 input size와 output size가 같기 때문에 boundary artifacts가 생긴다.

이를 방지하기 위해 zero padding을 이용했다.

 

 

Integration of Residual Learning and Batch Normalization for Image Denoising

위 그림(fig. 1)을 보면 original mapping $\mathcal{F}(\mathbf{y})$가 $\mathbf{x}$를 예측하고, 동시에 residual mapping $\mathcal{R}(\mathbf{y})$가 $\mathbf{v}$를 예측한다.

Original mapping이 identity mapping과 같을 때 residual mapping을 optimize하기 더 쉬워진다.

Noisy한 $\mathbf{y}$는 residual인 $\mathbf{v}$보다 clean한 $\mathbf{x}$와 더 가깝기 때문에 $\mathcal{F}(\mathbf{y})$가 $\mathcal{R}(\mathbf{y})$보다 identity mapping에 가깝다.

 

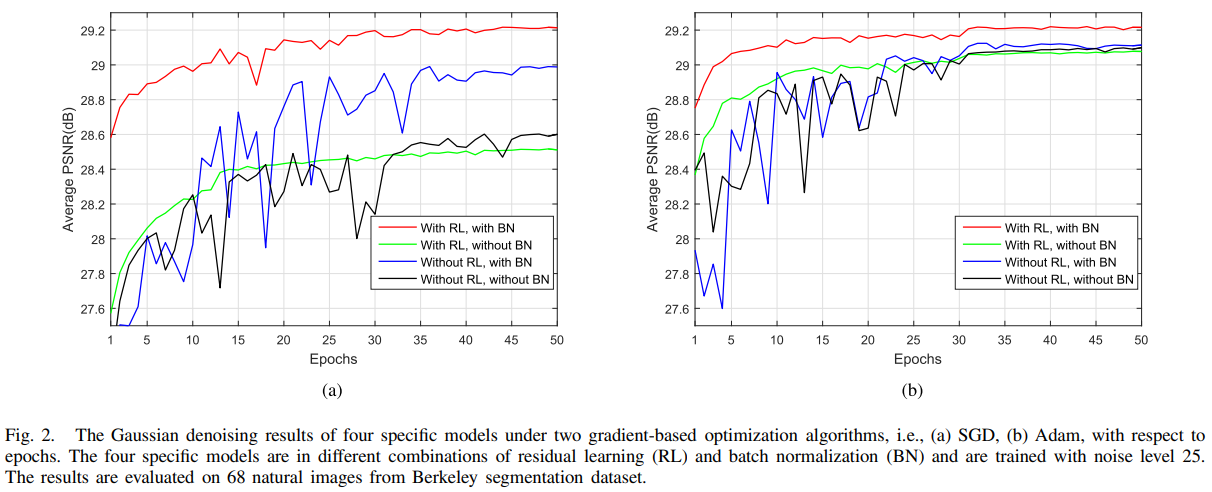
위 그림(fig. 2)을 보면 residual learning(RL)을 사용했을 때 더 빨리 안정적으로 converge된다는 것과, RL과 BN을 같이 사용했을 때 그 성능이 더 좋아진다는 것을 알 수 있다.

 

Connection with TNRD

TNRD는 다음과 같은 문제를 해결하기 위한 것이다.

$\displaystyle \min_\mathbf{x} \Psi(\mathbf{y}-\mathbf{x}) + \lambda \sum^K_{k=1}\sum^N_{\rho=1}\rho_k((\mathbf{f_k} * \mathbf{x})_{\rho})$

$\mathbf{f_k} * \mathbf{x}$: conv of the image $\mathbf{x}$ and the $k$-th filter kernel $\mathbf{f_k}$

Gaussian denoising을 할 때 $\Psi(\mathbf{z})={1 \over 2}||\mathbf{z}||^2$로 뒀다.

위 식을 정리하다보면 아래와 같이 된다.

$\mathbf{v}_1 = \mathbf{y} - \mathbf{x}_1 = \alpha \lambda \displaystyle \sum^K_{k=1}(\mathbf{\hat{f}}_k * \phi(\mathbf{f}_k * (\mathbf{y}))$

여기서 $\phi_k(·)$는 conv feature map에 적용된 point-wise nonlinearity로 볼 수 있기 때문에 위 수식은 2층으로 이루어진 CNN이라 볼 수 있다.

따라서 Fig. 1에서 제안하는 CNN 구조는 3가지 측면에서 발전된 TNRD라 할 수 있다.

1) influence function을 ReLU로 바꿔 CNN 학습이 더 잘되게 함

2) image 특성을 더 많이 담기 위해 CNN의 깊이를 늘림

3) BN으로 학습이 더 잘되게 함

 

Extension to General Image Denoising

MLP, CSF나 TNRD와 같은 Gaussian denoising 방법들은 fixed noise level에 대한 모델들이다.Unknown noise에 대해서 Gaussian denoising을 할 때 주로 사용하는 방법은, noise level을 측정한 후 해당 noise level에 맞게 학습 된 모델을 사용하는 것이다.이런 방법을로 SISR이나 JPEG denoising과 같은 non-Gaussian noise에도 적용할 수 있다.

---

Experimental Results

SISR에 대해서도 좋은 성능을 보이고,

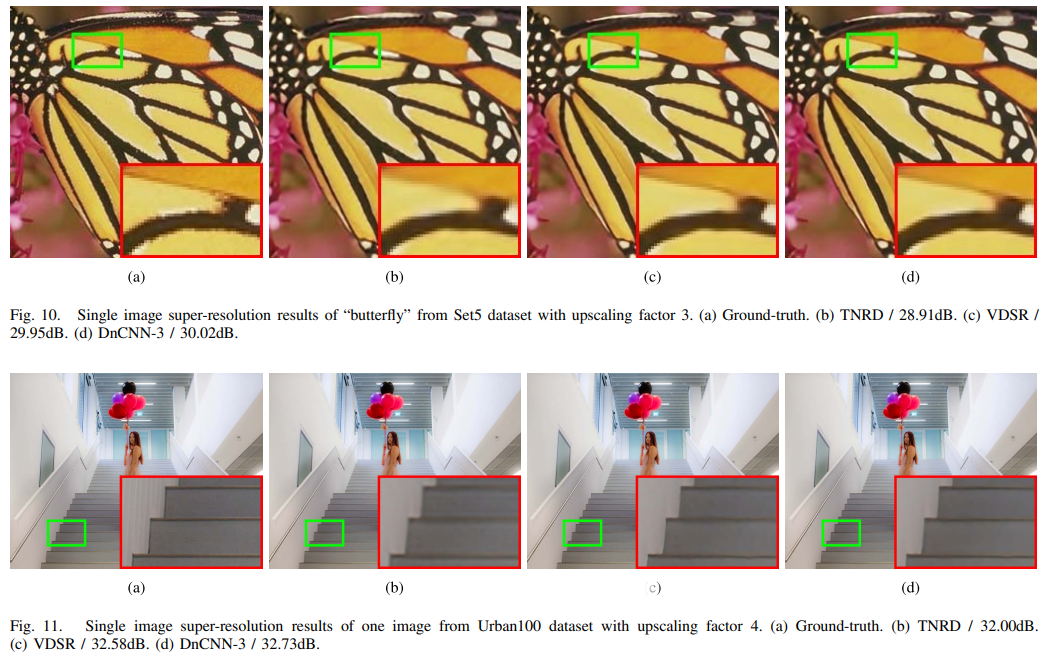
JPEG image deblocking에 대해서도 좋은 성능을 보인다.

---

Conclusion

본 논문에서는 noisy image로부터 noise를 분류하기 위해 residual learning을 사용한, image denoising을 위한 CNN을 제안한다.

BN과 RL을 사용해서 학습 속도를 높였다.

특정 noise level에 대해서만 학습하는 기존의 모델들과 달리, DnCNN은 한 모델로 여러 noise scale에 대한 blind Gaussian denoising을 할 수 있고, 이는 Gaussian denoising에만 국한되지 않고, SISR, JPEG artifacts에도 적용된다.

---

Reference

Zhang, Kai, et al. "Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising." IEEE transactions on image processing 26.7 (2017): 3142-3155.